Consolidation
Process
Calculation methods
Different approaches to calculate the amount of consolidation are supported (Bootsma, Kooi, and Erkens 2020): the Koppejan and Isotache models.
Koppejan model
The Koppejan (Civil Engineering) 1996) model…
Isotache model
The Isotache model (Den Haan 1996; Kooi et al. 2018) has become the recommended model for settlement modelling in the Netherlands since about one decade. It overcomes limitations of the Koppejan model but requires more sensitive parameter tuning to avoid spurious effects of anomalously high creep rates and initial subsidence rates. Total strain \(\varepsilon\) (relative height loss) of a voxel for a time step \(\Delta{t} = t^n-t^{n-1}\) consists of an elastic part and an inelastic part. The latter follows from a rate-law (viscous behaviour) that is referred to as creep. The model uses three compression parameters: swelling constant \(a\), compression constant \(b\), secondary compression constant \(c\). The elastic strain increment is obtained from:
\[ \Delta\varepsilon_{e} = a \ln\left(\frac{\sigma^{\prime(n)}}{\sigma^{\prime(n-1)}}\right) \tag{1}\]
where \(\sigma^{\prime}\) is the effective stress. Creep strain is governed by intrinsic time:
\[ \tau = \tau_{ref}OCR^{\frac{b-a}{c}}; \; OCR = \sigma_p^{\prime} / \sigma^{\prime} \tag{2}\]
where \(OCR\) is the overconsolidation ratio, \(\sigma_p^{\prime}\) the preconsolidation stress and \(\tau_{ref}\) a reference intrinsic time of 1 d.
The creep strain is calculated from the following set of relationships (Equation 3 and 4): \[ \Delta\varepsilon_{cr} = c \ln\left(\frac{\tau^n}{\tau^*}\right); \; \tau^n = \tau^* + \Delta{t} \tag{3}\]
\[ \tau^* = \tau^{n-1}\left(\frac{\sigma^{\prime(n-1)}}{\sigma^{\prime(n)}}\right)^\frac{b-a}{c} \tag{4}\]
DrainingABCIsotache
ABCIsotache
Effective stress development
The Koppejan and isotache compression models are combined with a module that handles effective stress development. Stresses are evaluated for the center-depth of voxels. Presently, effective stress calculation uses the degree-of-consolidation approach of Terzaghi (e.g. Verruijt 2001). The equilibrium effective stress for fully drained (end of primary consolidation) conditions is calculated as the difference of total stress and equilibrium pore pressure:
\[ \sigma_{eq}^{\prime} = \sigma - p_{eq} \tag{5}\]
Total stress is obtained from the overburden weight, where specific weight varies per lithology (sand, clay, peat). A saturated and unsaturated specific weight is specified. Specific weight increases with volume loss by compression. Equilibrium pore pressure (\(p_{eq}\)) is obtained from the equilibrium hydraulic head (\(h_{eq}\)):
\[ p_{eq} = \frac{h_{eq}-z}{\gamma_{w}} \tag{6}\]
where \(\gamma_{w}\) is the specific weight of water and \(z\) the elevation head relative to the Dutch ordinance level. Equilibrium head is currently based on linear interpolation between the head of the aquifer which underlies the Holocene confining layer and the momentary phreatic water table. That is, more complex head variation over the Holocene voxel stack in case of vertical seepage in combination with vertically varying hydraulic conductivity is currently neglected. Note that the approach includes effective stress reduction (load reduction) due to drowning; during a stress period in which both water table and aquifer head are constant, the equilibrium pore pressure of the voxels tends to slowly increase due to consolidation-related subsidence which lowers the elevation head \(z\).
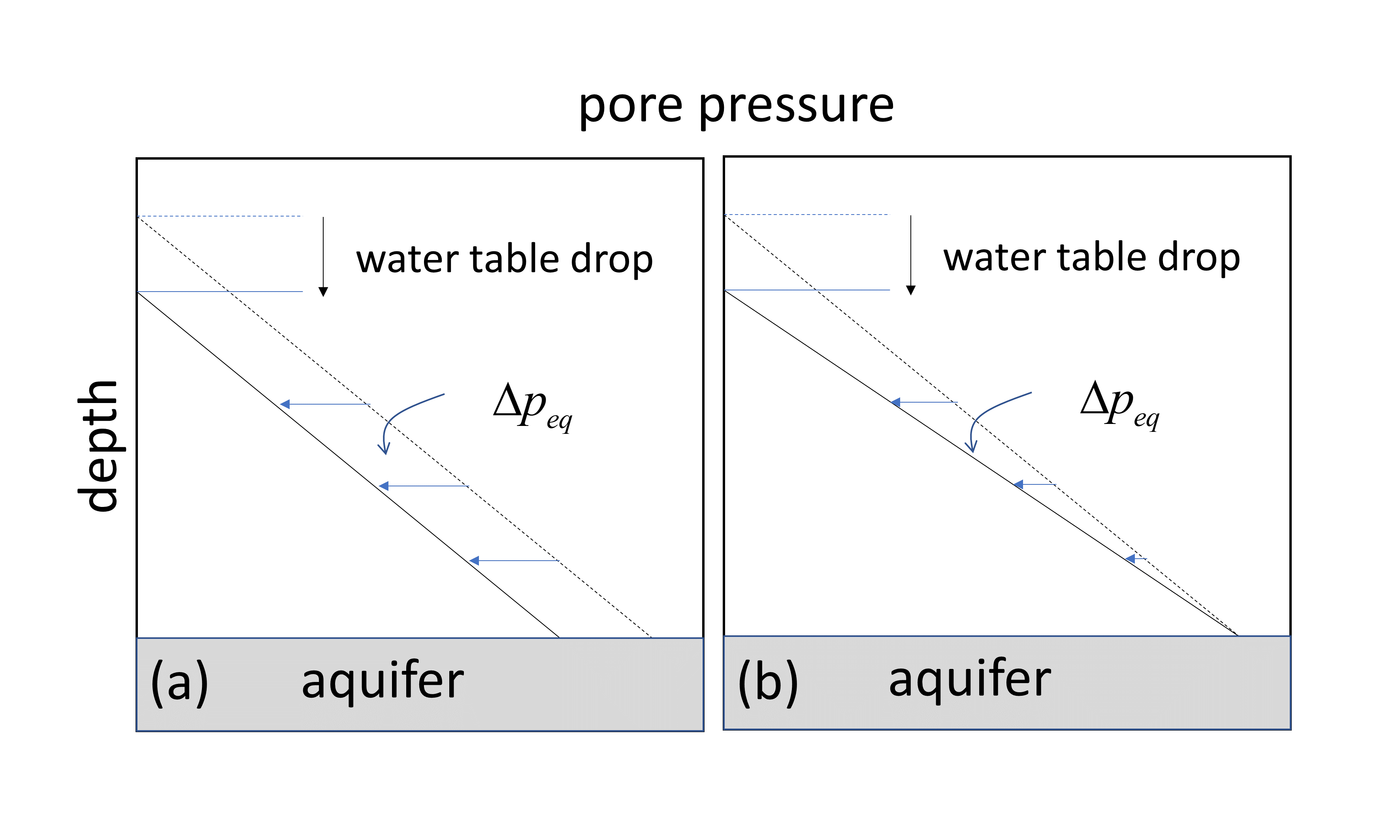
A water table lowering event at the start of a stress period corresponds to a “load” \(\sigma_{eq}^{\prime} = \Delta\sigma - \Delta{p_{eq}}\). Currently two options are available for the way \(\Delta{p_{eq}}\) is handled (Fig. 1). The change in total stress Δσaccounts for the reduction of overburden weight when the unsaturated specific weight is less than the saturated specific weight. In the time steps within the stress period, the load \(\Delta\sigma_{eq}^{\prime}\) is gradually transferred to \(\sigma\) using the degree-of-consolidation \(U\):
\[ \sigma^{\prime(n)} = \sigma^{\prime(n-1)} + \Delta{U}\Delta\sigma_{eq}^{\prime(n-1)}; \; \Delta{U} = U^{(n)} - U^{n-1} \]
\[ U(t) = \left[\frac{T^3}{T^3+0.5}\right]^{1/6}; T = \frac{c_vt}{L^3} \]
where \(T\) is the non-dimensional consolidation time, \(c_v\) the consolidation coefficient and \(L\) the length scale of two-sided drainage. Presently, \(L\) is set equal to the thickness of a voxel (which tends to decrease with time).